●●● crystal structures in the PAULING FILE
●● features
An individual structure entry contains data reported for a particular phase in a particular literature reference. The minimal requirement is a complete set of published cell parameters, assigned to a phase of known composition. Whenever published data are available, the crystallographic data also include atom coordinates, (an)isotropic displacement parameters and diffraction lines, and are accompanied by information concerning preparation, experimental conditions, characteristics of the sample, phase transitions, variations of the cell parameters with respect to temperature, pressure and composition, etc. In order to give an approximate idea of the actual structure, a complete set of atom coordinates and site occupancies is proposed for database entries where a prototype could be assigned, but atom coordinates were not refined. The crystallographic data are stored as published, but have also been standardized according to the method proposed by Parthé and Gelato [1], using the program STRUCTURE TIDY [2], and, when relevant, further adjusted so that the data for isotypic entries can be directly compared [3]. Derived data include atomic environments of individual atom sites, based on the maximum gap method [4] , the Niggli cell and assignment of structure classes. The database entries have been checked for inconsistencies within the database entry (e.g. chemical elements, charge balance, interatomic distances, space group, symmetry constraints), and comparing different database entries (e.g. cell parameters and atom coordinates of isotypic compounds) with a program package counting more than 30 modules [5]. For 5% of the database entries one or more misprints in the crystallographic data as published were detected and corrected. Warnings concerning remaining short interatomic distances, deviations from the nominal composition, etc., are added in remarks. SI units are used everywhere and the crystallographic terms follow the recommendations by the International Union of Crystallography [6].
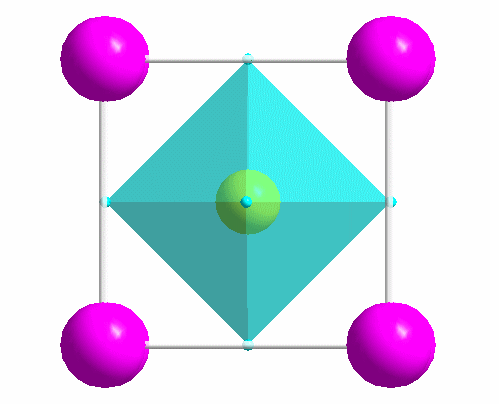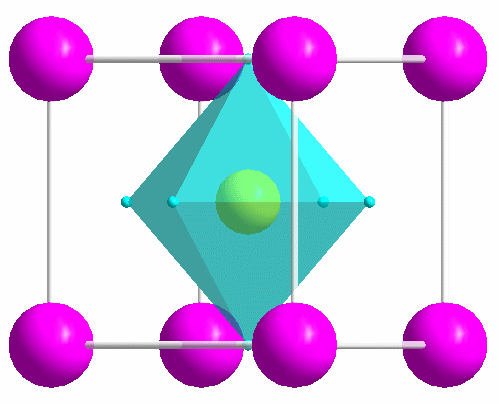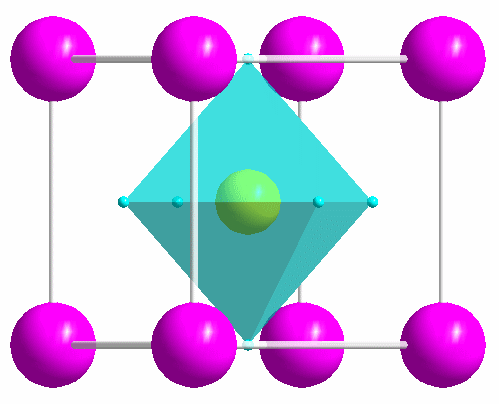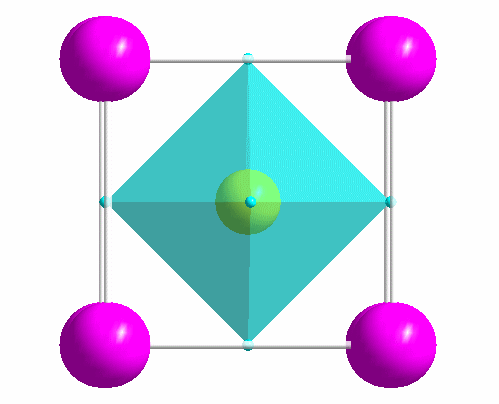 |
One of the most common structure types: perovskite (idealized CaTiO3). |
●● data selection
All data are extracted from primary literature. Thesis works are not considered and conference abstracts are processed only in exceptional cases. When available, supplementary material deposited as cif files or in other formats is used as data source. Approx. 10% of the processed documents exist in an original and a translated version; duplicates have been carefully avoided and both references are stored. Crystallographic data derived by ab-initio calculations have been considered only when confirmed by experimental studies.
Distinct database entries are created for all complete refinements reported in a particular paper. For data without published atom coordinates, a database entry has been prepared for each chemical system and prototype (a distinct phase in the definition used here). For an investigation of a compound through a temperature-induced phase transition there will be two database entries, one for the ht modification and one for the rt modification, both containing remarks about the temperature dependence of the cell parameters within their respective ranges of existence. For a continuous solid solution between two ternary compounds, there will be three database entries: one for each ternary border compound and one for the quaternary system, the latter with a remark describing the composition dependence of the cell parameters. For the choice of retrievable cell parameters, preference is given to values determined under ambient conditions.
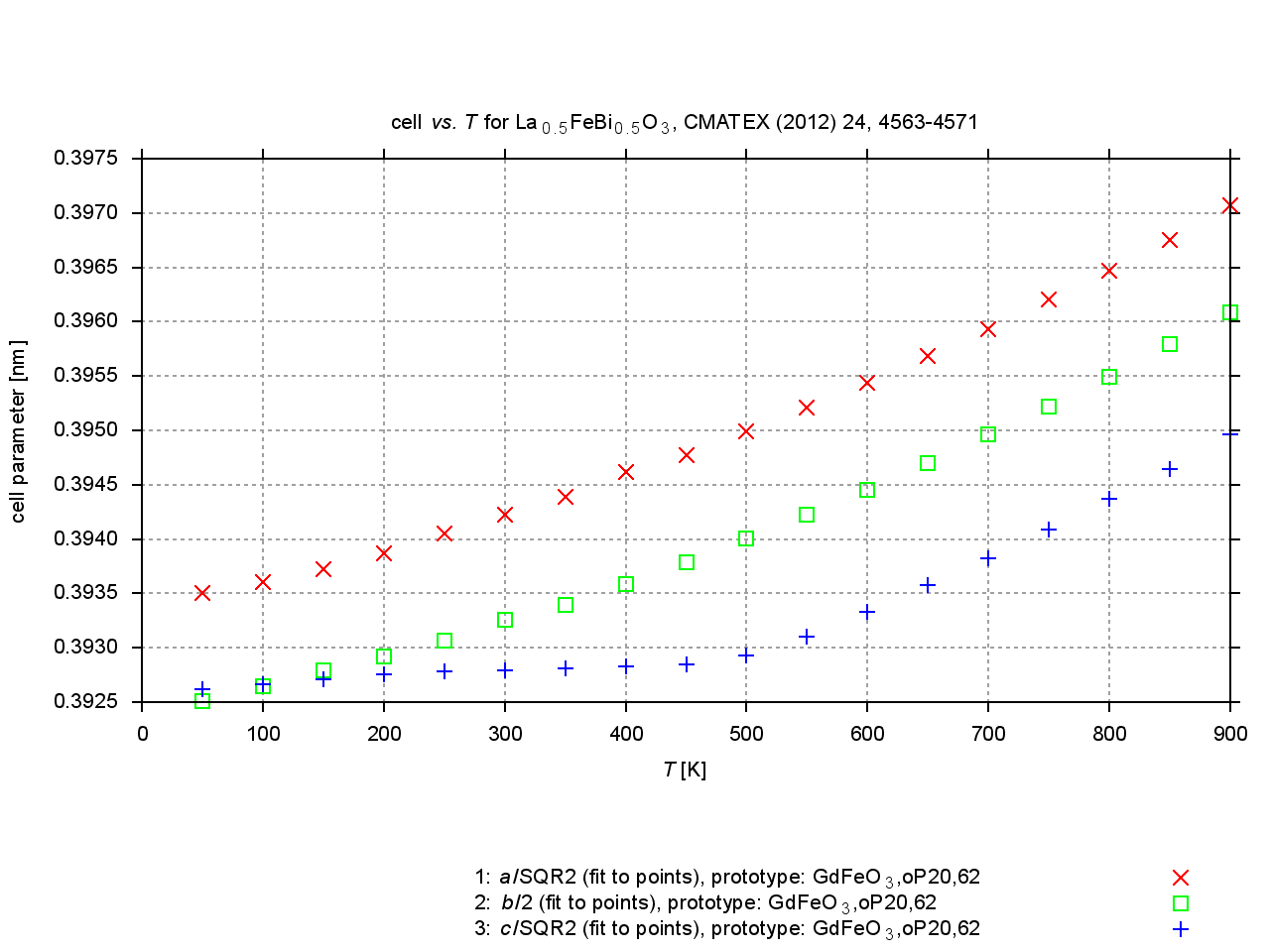
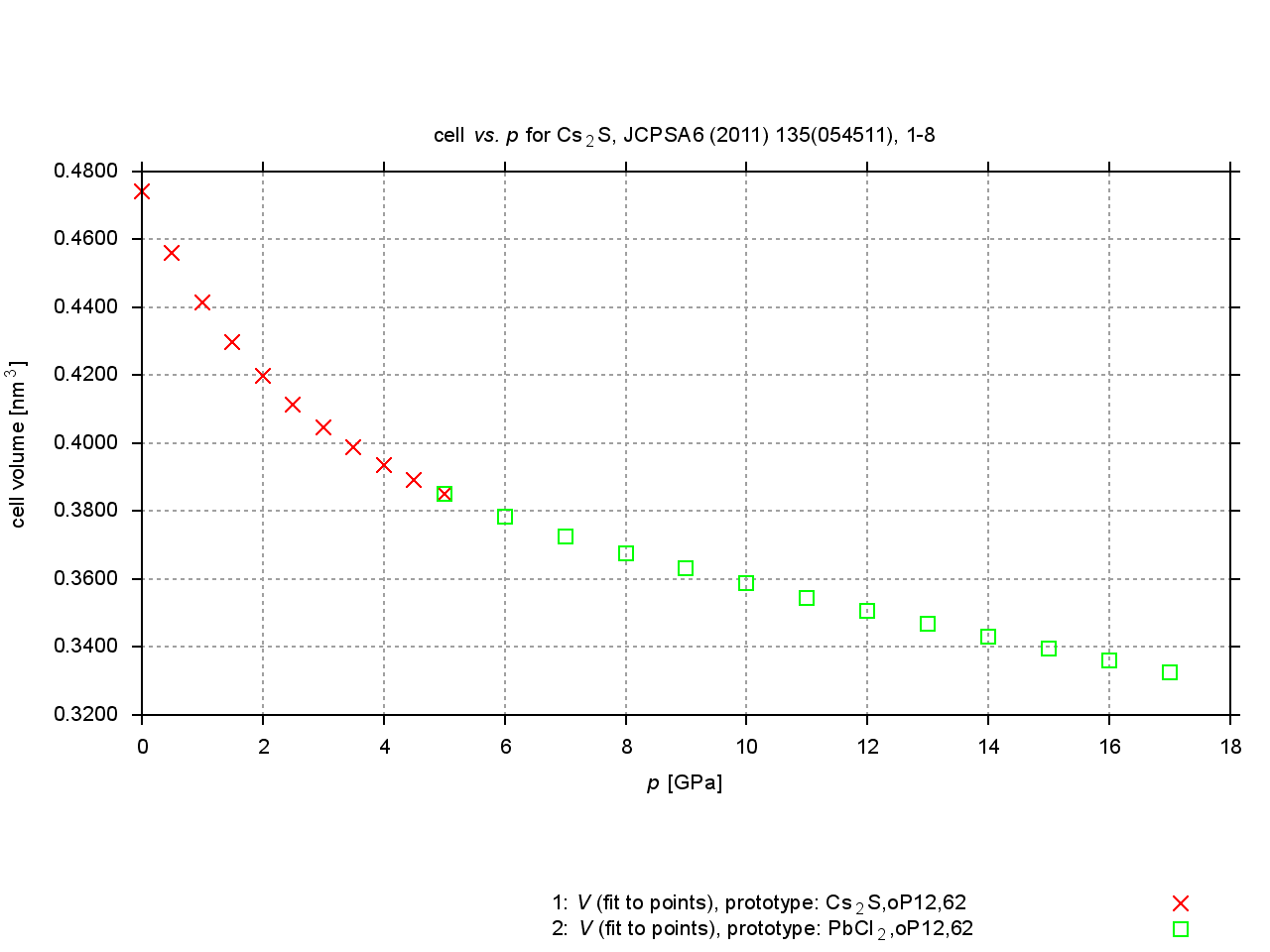
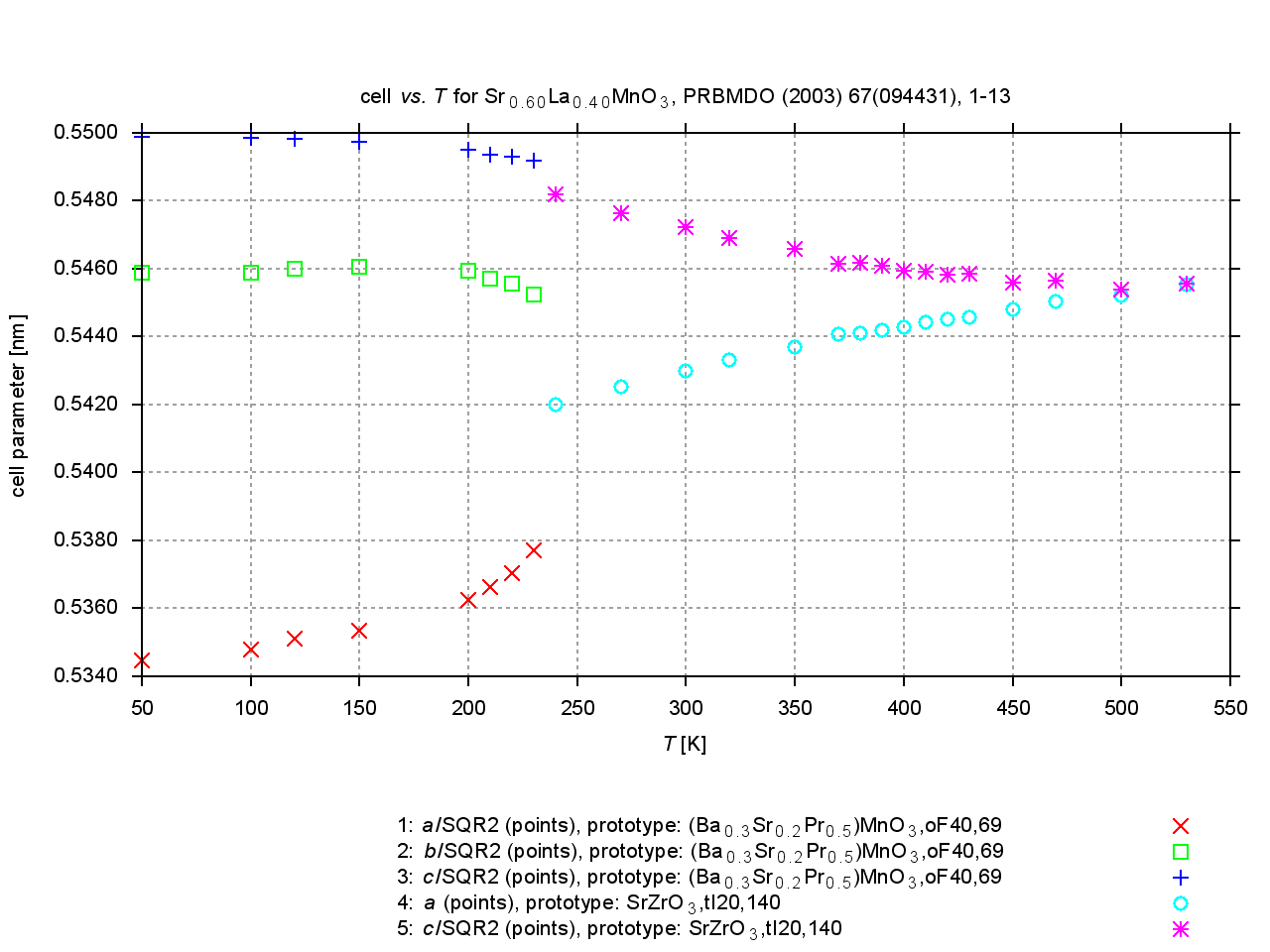
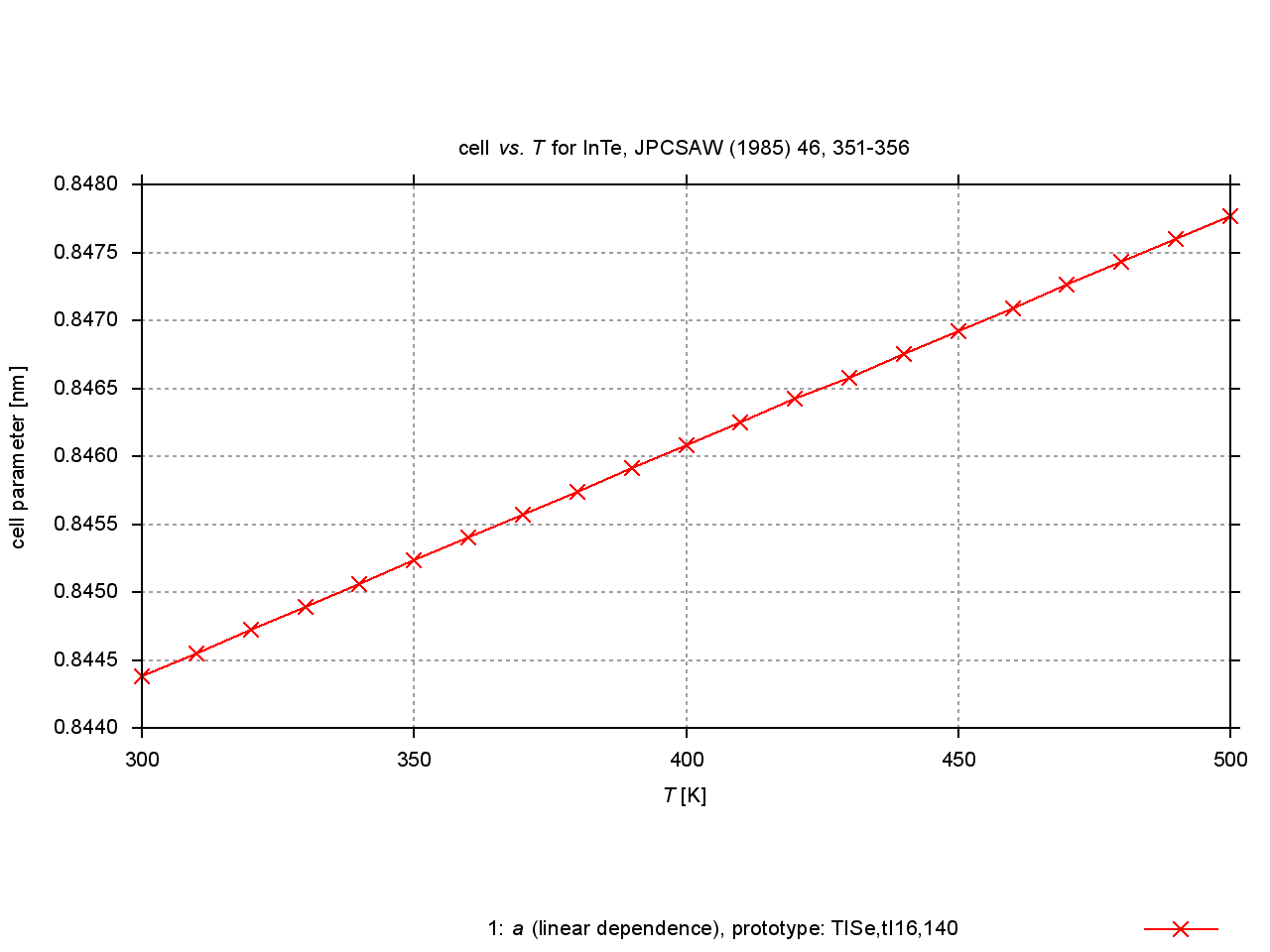
Since 2009, values are extracted from plots of cell parameters (or functions of these) versus temperature, pressure or composition. New figures are produced to illustrate thermal expansion, phase transitions, or compression under pressure, and sets of standardized cell parameters are stored.
|
|
|
|
●●● statistics
●● distribution according to journal
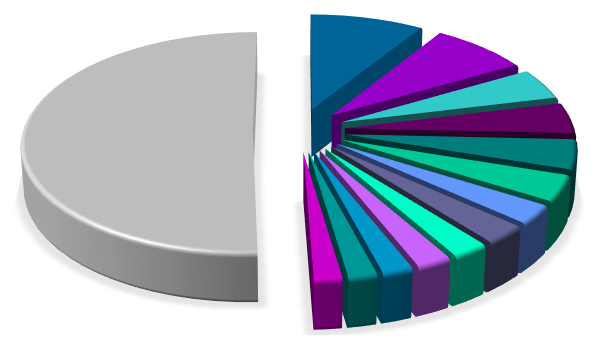
|

|
● journals
Journal of Alloys and Compounds Journal of Solid State Chemistry Inorganic Chemistry Acta Crystallographica Physical Review B Zeitschrift für Anorganische und Allgemeine Chemie Inorganic Materials Russian Journal of Inorganic Chemistry Chemistry of Materials Journal of Magnetism and Magnetic Materials Materials Research Bulletin Zeitschrift für Kristallographie American Mineralogist others 135'197 publications processed 03.2024 |
●● distribution according to publication year

●● distribution according to chemical class
| ● 1 or 2 elements | ● 3 elements | ● 4 or more elements | |
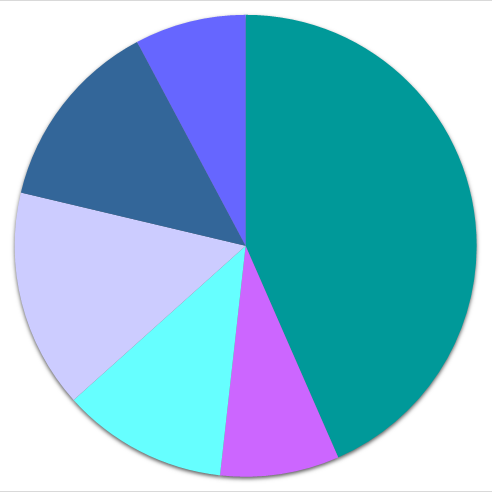 72'015 |
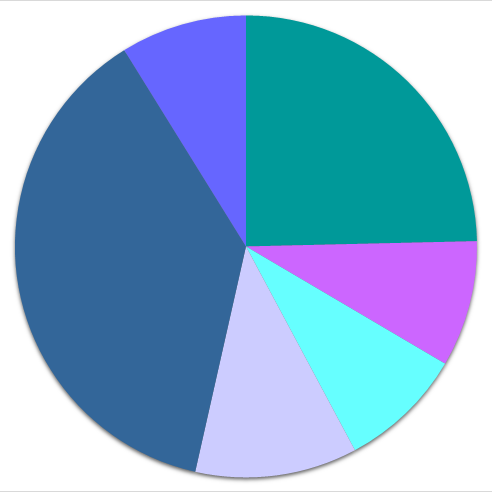 156'108 |
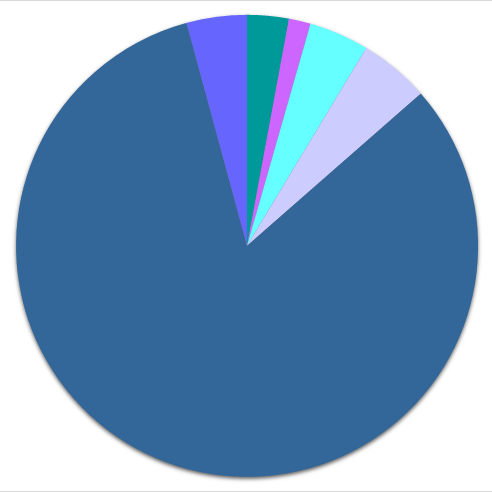 195'626 |

|
●●● structure prototypes
●● definition
The structure type is a well-known concept in inorganic chemistry where a large number of compounds often crystallize with very similar atom arrangements. The compilation Strukturbericht [7] started to catalogue crystal structures into types, named by codes such as A1, B1 or A15. Though these notations are still in use, structure types are now generally referred to by the name of the compound for which this particular atom arrangement was first identified, i.e. for the types enumerated above: Cu, NaCl, Cr3Si. The PAULING FILE uses a longer notation, which includes also the Pearson symbol [8] and the space group number [6]: Cu,cF4,225; NaCl,cF8,225; Cr3Si,cP8,223. All data sets with published atom coordinates in the PAULING FILE have been classified into structure prototypes, following the criteria defined in TYPIX [9]. According to this definition, isotypic compounds must crystallize in the same space group, have similar cell parameter ratios, and occupy the same Wyckoff positions in the standardized description, with the same or similar values of the atom coordinates. When possible, a prototype has been assigned also to data sets without refined atom coordinates.
●● common prototypes
| select a prototype |
●●● terminology
The atoms vibrate around their average positions with an amplitude that increases with increasing temperature. As a result, the intensity of the diffracted beam is reduced. In their anisotropic form the displacement parameters are expressed by a diagonal matrix. Several expressions are found in the literature (a*,b*,c* are the translation vectors in reciprocal space and h,k,l the Miller indexes of a reflection in the diffraction pattern):
| parameter | expression | SI unit |
| βi j | exp[−(β11h2 + β22k2 + β33l 2 + 2β12hk + 2β13hl + 2β23kl)] | (dimensionless) |
| Ui j | exp[−2π2(U11h2a*2 + U22k2b*2 + U33l2c*2 + 2U12hka*b* + 2U13hl a*c* + 2U23klb*c*)] | nm2 |
| Bi j | exp[−1/4(B11h2a*2 + B22k2b*2 + B33l2c*2 + 2B12hka*b* + 2B13hla*c* + 2B23klb*c*)] | nm2 |
The point symmetry of the atom site imposes constraints on the matrix.
The positions of the atoms are conventionally given in fractional coordinates x y z, referring to the cell parameters a, b and c, respectively (translation units of the lattice) and adopt values 0 ≤ x,y,z < 1. One triplet x y z is given for each set of symmetry-related positions (atom site). The positions of the other atoms in the unit cell belonging to the same site can be obtained by applying the symmetry operations defined by the space group, listed in the International Tables for Crystallography, Vol. A [6]. The atom positions in an idealized, infinite structure are obtained by applying in addition the translation symmetry defined by the cell vectors (x±Na y±Nb z±Nc, where Na, Nb, Nc are integers).
The Atomic Environment (AE), also called coordination polyhedron, describes the arrangement of the nearest neighbors to an atom site. The AEs stored in the PAULING FILE have been assigned using the method of Brunner and Schwarzenbach [4], where the interatomic distances between an atom and its neighbors are plotted in a next-neighbor histogram (NNH), without distinguishing different chemical elements.
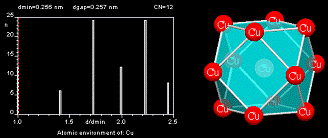
The atoms to the left of the maximum gap in the diagram belong to the AE of the central atom (maximum gap rule) and the Atomic Environment Type (AET) is constructed with these atoms. The AET shown in the figure is a cuboctahedron. The most common AETs are listed below.
| coordination number | atomic environment type |
| 1 | single atom |
| 2 | collinear |
| 2 | non-collinear |
| 3 | coplanar triangle |
| 3 | non-coplanar triangle |
| 4 | coplanar square |
| 4 | tetrahedron |
| 5 | square pyramid |
| 6 | octahedron |
| 6 | pentagonal pyramid |
| 6 | trigonal prism |
| 7 | monocapped trigonal prism |
| 8 | square antiprism |
| 8 | square prism (cube) |
| 9 | tricapped trigonal prism |
| 10 | bicapped square antiprism |
| 12 | anticuboctahedron |
| 12 | cuboctahedron |
| 12 | icosahedron |
| 13 | pseudo Frank-Kasper (13) |
| 14 | rhombic dodecahedron |
| 14 | 14-vertex Frank-Kasper |
| 16 | 16-vertex Frank-Kasper |
| 20 | pseudo Frank-Kasper (20) |
The lattice planes (planes defined by three points of the translation lattice) act as "mirrors" with respect to a radiation having a wavelength of the same order of magnitude as the translation lattice itself. The Bragg angle θ is the angle between the reflecting plane and the diffracted beam, identical to the angle between the reflecting plane and the incident beam. It expresses the angular position of the peaks in the diffraction pattern and is related to the interplanar spacing d of the translation lattice through the Bragg law:
| nλ = 2d sin(θ) | where n is the order of the reflection and λ is the wavelength. |
The translation lattice is a mathematical abstraction built up from points having exactly the same environment. The translation unit (unit cell) is a parallelepiped obtained by joining eight lattice points. Any crystal structure can be described by a primitive cell, i.e. a cell containing no more lattice points than those at the vertices of the parallelepiped. By convention, a multiple cell that respects the symmetry of the structure is, however, generally preferred. An orthorhombic all-face centered cell is, for instance, preferred to a primitive triclinic cell for a structure presenting three mutually perpendicular 2-fold axes (condition for orthorhombic system).
code |
centering type of the cell | translations |
P |
primitive | (x y z + 0 0 0) |
| A | A-face centered | (x y z + 0 0 0, 0 1/2 1/2) |
| B | B-face centered | (x y z + 0 0 0, 1/2 0 1/2) |
| C | C-face centered | (x y z + 0 0 0, 1/2 1/2 0) |
| F | all-face centered | (x y z + 0 0 0, 0 1/2 1/2, 1/2 0 1/2, 1/2 1/2 0) |
| I | body centered | (x y z + 0 0 0, 1/2 1/2 1/2) |
| R | rhombohedrally centered |
(x y z + 0 0 0, 2/3 1/3 1/3, 1/3 2/3 2/3) for obverse setting
(x y z + 0 0 0, 2/3 1/3 2/3, 1/3 2/3 1/3) for reverse setting |
The letter S (side-face centered), grouping A-, B- and C-face centered cells, is recommended by the International Union of Crystallography [10] when used in classifications, since this notation is independent of the actual space group setting. Some combinations centering type - crystal system being impossible or equivalent to others, there exist 14 distinct Bravais lattices: aP, mP, mS, oP, oS, oF, oI, tP, tI, hP, hR, cP, cF, cI.
The cell parameters (also called lattice parameters, lattice constants, translation periods) define the translation unit of the crystal structure. By convention, the smallest unit cell in agreement with the symmetry of the structure is preferred. For crystal systems higher than triclinic, certain parameters are constrained to particular values and only the refinable parameters are usually specified.
| crystal system | constraints | refinable cell parameters |
| triclinic = anorthic | none | a, b, c, α, β, γ |
| monoclinic | two angles = 90° | a, b, c, one angle |
| orthorhombic | α, β, γ = 90° | a, b, c |
| tetragonal | α, β, γ = 90°; a = b | a, c |
|
trigonal:
hexagonal cell rhombohedral cell |
α, β = 90°, γ = 120°; a = b α = β = γ; a = b = c |
a, c a, α |
| hexagonal | α, β = 90°, γ = 120°; a = b | a, c |
| cubic | α, β, γ = 90°; a = b = c | a |
The cell parameters a, b, c are in the PAULING FILE expressed in the SI unit nm: 1 nm = 10 Å = 1000 pm.
The seven crystal systems are defined by the existence of particular symmetry elements in the structure. For each crystal system a unit cell of a particular shape is by convention preferred.
| crystal system | required symmetry element(s) | conventional unit cell |
| triclinic = anorthic | identity and possibly an inversion center | a parallelepiped |
| monoclinic | a 2-fold axis | a straight prism with rhombic base |
| orthorhombic | three mutually perpendicular 2-fold axes | a straight prism with rectangular base |
| tetragonal | a 4-fold axis | a straight prism with square base |
| trigonal | a 3-fold axis |
one third of a straight prism with hexagonal base
or a rhombohedron |
| hexagonal | a 6-fold axis | one third of a straight prism with hexagonal base |
| cubic | four 3-fold axes forming angles of 70.53° with each other | a cube |
A mirror plane is equivalent to a 2-fold inversion axis. Note that the crystal system is defined by the symmetry of the structure and not by the shape of the unit cell, e.g. the unit cell describing a triclinic structure can be a perfect cube.
The space groups represent the 230 unique combinations of symmetry operations possible in three-dimensional space. In the Hermann-Mauguin notation each space group (setting) is represented by a series of characteristic symmetry elements. The first, upper-case, character indicates the centering type of the Bravais lattice. The order of the other characters is differently defined for each type of crystal system and unit cell.
| crystal system | direction for 1st operation | direction for 2nd operation | direction for 3rd operation | example |
| triclinic = anorthic | — |
|
|
P -1 |
|
monoclinic:
long symbol short symbol |
[1 0 0] unique axis |
[0 1 0] |
[0 0 1] |
P 1 2/m 1 P 2/m |
| orthorhombic | [1 0 0] | [0 1 0] | [0 0 1] | C m c e |
| tetragonal | [0 0 1] | [1 0 0] | [1 -1 0] | I 4/m c m |
|
trigonal:
hexagonal cell rhombohedral cell |
[0 0 1] [1 1 1] |
[1 0 0] [1 -1 0] |
|
P 3 m 1 R 3 m |
| hexagonal | [0 0 1] | [1 0 0] | [1 -1 0] | P 63/m c m |
| cubic | [1 0 0] | [1 1 1] | [1 -1 0] | P n -3 m |
Example: Fm-3m
- cubic
- all-face centered Bravais lattice
- mirror planes m perpendicular to the three crystallographic axes a, b and c
- three-fold inversion axes -3 along the four body diagonals
- mirror planes m perpendicular to the six face diagonals
The Hermann-Mauguin symbol defines not only the space group, but the space group setting. For example, Pnma, Pmcn, Pbnm, Pnam, Pcmn, and Pmnb represent different settings of space group No. 62 [6], corresponding to different rotations/permutations of the cell vectors. The example shows the relation between the space group setting and the choice of the unit cell of an orthorhombic perovskite.
| Hermann-Mauguin symbol | a [nm] | b [nm] | c [nm] | rotation/permutation |
| Pnma | 0.561 | 0.767 | 0.535 | a,b,c |
| Pmcn | 0.767 | 0.535 | 0.561 | b,c,a |
| Pbnm | 0.535 | 0.561 | 0.767 | c,a,b |
| Pnam | 0.561 | 0.535 | 0.767 | -a,c,b |
| Pcmn | 0.535 | 0.767 | 0.561 | c,b,-a |
| Pmnb | 0.767 | 0.561 | 0.535 | b,-a,c |
In the PAULING FILE the crystallographic data are presented as published and standardized with the program STRUCTURE TIDY [2], where they always refer to the space group setting presented in the International Tables for Crystallography [6], i.e. Pnma for space group No. 62.
The interplanar spacing d is the distance between two neighboring parallel lattice planes, i.e. planes containing three points (thus an infinite number of points) of the translation lattice. Families of parallel lattice planes are identified by Miller indices h k l. For cubic symmetry dhkl = a / (h2 + k2 + l2)1/2, where a is the cell parameter. The interplanar spacing is related to the Bragg angle, i.e. the angular position of the corresponding peak in the diffraction pattern, through the Bragg law:
| nλ = 2d sin(θ) | where n is the order of the reflection and λ is the wavelength. |
The displacement parameter expresses the magnitude of the displacement around the average atom position. It is also referred to as the temperature factor, since the amplitude of the displacement increases with increasing temperature. Two different expressions are commonly found in the literature:
| parameter | expression | SI unit |
| U | exp[−8π2U(sin(θ)/λ2] | nm2 |
| B = 8π2U | exp[−B(sin(θ)/λ2] | nm2 |
Equivalent isotropic displacement parameters can be computed from sets of anisotropic displacement parameters.
The Laue indexes h k l are used to designate the reflections in the diffraction pattern. Contrary to the Miller indexes, which are also called h k l but by definition are limited to low digits, the Laue indexes can take any integer value. In the PAULING FILE, in agreement with general practice, the indexes used in powder patterns are referred to as Miller indexes.
The Miller indexes h k l are used to designate families of parallel lattice planes, directions, crystal faces and forms. The Miller indexes corresponding to a family of parallel lattice planes can be found by carrying out the following operations:
1. determine the fractional coordinates of the intersections with the three crystallographic axes
2. invert these numbers
3. multiply the resulting number, if necessary, to obtain three integers
The expression [0 0 1] defines an axis, <0 0 1> all symmetry-equivalent directions, (0 0 1) a plane and {0 0 1} all symmetry-equivalent planes.
A crystal structure is conventionally described by the smallest unit cell that respects the symmetry of the structure. Such a cell sometimes contains several lattice points. A reduced cell is always primitive and the Niggli cell vectors a, b, c must satisfy the conditions listed below.
|
a·a
≤ b·b ≤ c·c
|b·c| ≤ ½ b·b |a·c| ≤ ½ a·a |a·b| ≤ ½ a·a |
|
| ●● Type I: (a·b)(b·c)(c·a) > 0 | ●● Type II: (a·b)(b·c)(c·a) ≤ 0 |
|
b·c
> 0
a·c > 0 a·b > 0 which implies α, β, γ > 90° |
|b·c| + |a·c| + |a·b| ≤ ½ (a·a + b·b)
b·c ≤ 0 a·c ≤ 0 a·b ≤ 0 which implies α, β, γ ≤ 90° |
In case of equality, e.g. a·a = b·b, special conditions are applied. The complete set of conditions can be found in the International Tables for Crystallography, Vol. A [6].
The Niggli cell parameters in the PAULING FILE are computed by the program STRUCTURE TIDY [2].
The Pearson symbol, e.g. mP48, was introduced to classify intermetallic structures [8]. It is composed of three distinct parts, the first of which is a lower-case letter representing the crystal system.
| a | triclinic = anorthic |
| m | monoclinic |
| o | orthorhombic |
| t | tetragonal |
| h | hexagonal, trigonal |
| c | cubic |
This is followed by an upper-case letter designating the centering type of the Bravais lattice.
| code | centering type | translations |
| P | primitive | (x y z + 0 0 0) |
| S | side-face centered |
(x y z + 0 0 0, 0 1/2 1/2) for A-centered
(x y z + 0 0 0, 1/2 0 1/2) for B-centered (x y z + 0 0 0, 1/2 1/2 0) for C-centered |
| F | all-face centered | (x y z + 0 0 0, 0 1/2 1/2, 1/2 0 1/2, 1/2 1/2 0) |
| I | body centered | (x y z + 0 0 0, 1/2 1/2 1/2) |
| R | rhombohedrally centered |
(x y z + 0 0 0, 2/3 1/3 1/3, 1/3 2/3 2/3) for obverse setting
(x y z + 0 0 0, 2/3 1/3 2/3, 1/3 2/3 1/3) for reverse setting |
The last item is a number corresponding to the sum of the site multiplicities of all atom sites in the structure, which, for a structure without vacancies, is equal to the number of atoms in the unit cell. The similar term Pearson code is used when the number is defined as the number of atoms in the unit cell. The number may in the latter case be a non-integer, whereas the number in the Pearson symbol is always an integer. Throughout the PAULING FILE, the sum of multiplicities given for a trigonal structure with an R-lattice (rhombohedral) refers to the triple hexagonal cell, and is thus always a multiple of 3.
Different factors are proposed in the literature to express the degree of reliability of a structure refinement (F - structure factor, I - intensity, y - counts at a point of a powder pattern, sub o - observed, sub c - calculated):
| abbreviation | expression | name |
| R |
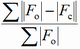 |
conventional R factor (F may be relaced by F2) |
| wR |
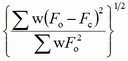 |
weighted R factor |
| Rp |
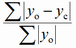 |
profile |
| wRp |
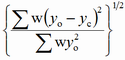 |
weighted profile |
| RB |
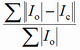 |
Bragg factor |
The term "residual", even if used less frequently, is more appropriate since the lower the R factor, the more reliable the structure proposal. It should be emphasized that a low R factor is not a guarantee for a correct structure.
The site multiplicity is the number of positions in the unit cell corresponding to a particular atom site. It can be derived by applying the symmetry operations of the space group. For atom sites situated on one or several symmetry elements, the site multiplicity is a fraction of the multiplicity of a site in general position.
The site symmetry is the point symmetry, i.e. symmetry implying no translational component, of a particular atom site. The site symmetry in the PAULING FILE is written following the notations used in the International Tables for Crystallography, Vol. A (1983) and later editions [6].
There exist 230 space groups, which represent the different possibilities to combine point and translational symmetry in three-dimensional space. Each combination is assigned a number in the International Tables for Crystallography, ranging from 1 for the triclinic space group P1 (no symmetry other than identity and translation) to 230 for the cubic space group Ia-3d, where each triplet in general position represents 96 atom positions in the unit cell. The space groups are commonly referred to by their Hermann-Mauguin symbol.
All crystallographic data in the PAULING FILE have been standardized following a method proposed by Parthé and Gelato [1], using the program STRUCTURE TIDY [2]. The standardization procedure applies criteria to select:
● the space group setting
● the cell parameters
● the origin of the coordinate system
● the representative atom coordinates
● the order of the atom sites
The coordinate system must be right-handed and refer to a space group setting defined in the International Tables for Crystallography [6], with the following additional constraints:
● triclinic space groups: Niggli cell
● monoclinic space groups: b-axis unique, "best" cell
● orthorhombic space groups: a ≤ b ≤ c, when not fixed by the space group setting
● trigonal space groups with R-lattice: triple hexagonal cell
● space groups with two origin choices: origin choice 2 (origin at inversion center)
● enantiomorphic space groups: smallest index of the relevant screw axis
For the 148 non-polar space groups there are between 1 and 24 possibilities to rotate, invert or shift the coordinate system, respecting the conditions listed above. For each possibility the standardization program prepares a complete data set where the representative triplet of each atom site must obey a series of eliminative conditions:
● first triplet in the International Tables for Crystallography [6]
● 0 ≤ x,y,z < 1
● minimum value of (x2 + y2 + z2)
● minimum value of x
● minimum value of y
● minimum value of z
For polar space groups similar data sets are prepared where one atom site after the other, belonging to the "lowest Wyckoff set" (set of Wyckoff sites containing the site of highest point symmetry - earliest letter in the alphabet) represented in the structure, fixes the origin on the polar axis. One of the data sets, prepared as described above, is selected based on the following eliminative conditions:
● minimum value of Γ = Σ(xj2 + yj2 + zj2)1/2 summing over all atom sites
● minimum value of Σxj summing over all atom sites
● minimum value of Σyj summing over all atom sites
● minimum value of Σzj summing over all atom sites
● minimum value of xn2 + yn2 + zn2 for the nth atom site
Finally, the atom sites are reordered according to the eliminative criteria:
● inverse alphabetic order of Wyckoff letters
● increasing x
● increasing y
● increasing z
Atom sites occupied by "protonic hydrogen atoms" are not taken into consideration when applying the criteria to select the appropriate setting, and are listed at the end of the data set.
An atom situated at a point outside any symmetry element is considered to be in general position. An atom located on one or several symmetry elements will belong to a site having higher point symmetry and lower site multiplicity. Within a particular space group, the general position and each of the distinct special positions are in the International Tables for Crystallography [6], designated by a lower-case letter, called the Wyckoff letter. These are attributed in alphabetic order, starting from a position with high point symmetry, and ending always with the general position. The combination site multiplicity - Wyckoff letter is generally referred to as Wyckoff position.
The Wyckoff sequence lists the Wyckoff letters of all, fully or partly occupied atom sites in the structure. The letters are written in inverse alphabetic order, a superscript number being added when a particular Wyckoff position is present more than once. According to the definition used here, isotypic compounds (compounds crystallizing with the same structure type) have the same Wyckoff sequence (are isopointal) if the crystallographic data have been standardized [9]. The inverse is not always true, i.e. structures having the same Wyckoff sequence are not necessarily isotypic.
references
[1] Parthé E., Gelato L.M. (1984), Acta Crystallogr. A40, 169-183; Parthé E., Gelato L.M. (1985), Acta Crystallogr. A41, 142-151; Parthé E., Cenzual K., Gladyshevskii R. (1993), J. Alloys Compd. 197, 291-301.
[2] Gelato L.M., Parthé E. (1987), J. Appl. Crystallogr. 20, 139-143.
[3] Berndt M., Thesis, University of Bonn, 1994; updates by O. Shcherban, SCC "Structure-Properties", 2006-2012.
[4] Brunner G.O., Schwarzenbach D. (1971), Z. Kristallogr. 133, 127-133; Daams J.L.C., in Intermetallic Compounds, Vol. 1: Principles, Eds. J.H. Westbrook, R.L. Fleischer, New York: John Wiley and Sons, 1994; Daams J.L.C., Villars P. (1997), J. Alloys Compd. 252, 110-142.
[5] Cenzual K., Berndt M., Brandenburg K., Luong V., Flack E., Villars P., ESDD software package, copyright Japan Science and Technology Agency, 2000; updates by O. Shcherban, SCC "Structure-Properties".
[6] International Tables for Crystallography, Vol. A, Ed. T. Hahn, Dordrecht: D. Reidel, 1983 and more recent editions.
[7] Ewald P.P., Hermann C., Strukturbericht, Leipzig: Akad. Verlagsgesellschaft M.B.H, 1931.
[8] Pearson W.B., Handbook of Lattice Spacings and Structure of Metals, New York: Pergamon, 1967.
[9] Parthé E., Gelato L., Chabot B., Penzo M., Cenzual K., Gladyshevskii R., Gmelin Handbook of Inorganic and Organometallic Chemistry, 8th Ed., TYPIX - Standardized Data and Crystal Chemical Characterization of Inorganic Structure Types, 4 volumes, Heidelberg: Springer, 1993, 1994.
[10] De Wolff P.P., Belov N.V., Bertaut E.F., Buerger M.J., Donnay J.D.H., Fischer W., Hahn T., Koptsik V.A., Mackay A.L., Wondratschek H., Wilson A.J.C., Abrahams S.C. (1985), Acta Crystallogr. A 21, 278-280.

